Programação Linear - Exercício de Aplicação (Modelo Matemático)
Olá bem-vindo ao curso da investigação operacional.
Vamos modelar um problema dado na sua estrutura de modelo matemático baseando-se em programação linear.
O PROBLEMA:
A empresa Kundiama produz material de escritório. Pretende
lançar novo modelo de secretária e estantes. Acredita-se que o mercado pode
absorver toda a produção de estantes, mas aconselha-se que se produza
mensalmente 160 unidades de secretarias. Ambos os produtos são produzidos nas
unidades de estampagem (UE) e de montagem e acabamento (UMA).
A disponibilidade mensal de cada unidade é de 720h na UE e
880h UMA. Cada secretária necessita de 2h na UE e 4h na UMA. A margem de lucros
previstos é 6,00kz para secretária e 3,00kz para as estantes.
Qual é o plano de produção mensal que maximiza a margem de lucros?
1º Passo:
IDENTIFICAR ELEMENTOS PRINCIPAIS DO PROBLEMA
Identificar o que a nossa empresa quer, neste caso, ela
quer produzir novo modelo de secretária
e estantes logo temos duas variáveis; a primeira variável que
é a secretária que chamaremos X1 e a quantidade de estantes que a
empresa quer produzir chamaremos por X2.
Voltando a verificar nosso problema, vimos que a produção de
estantes pode ser totalmente absorvida pelo mercado ou seja todas elas
podem ser compradas, já para secretárias aconselhou-se produzir apenas 160
unidades.
Estes dois materiais são produzidos em duas unidades uma
chamada de Unidade de Estampagem que representaremos pela EU, outra pela
Unidade de montagem e acabamento que está amaremos por UMA.
Nos diz ainda o problema que mensalmente na unidade de
estampagem os produtos demoram mais ou menos 720 horas. Já na unidade de
montagem e acabamento os elementos demoram 880 horas.
Unidade de Estampagem
Olhando agora especificamente para a unidade de estampagem,
vemos que para o primeiro produto secretária
ela necessita de duas horas (2h) a ser produzido. Como consideramos que o
produto secretária no seu modelo matemático será apresentado pela variável X1
então podemos escrever 2X1. O produto Estante
na mesma unidade de estampagem necessita de quatro horas (4h) para ser produzido o que pode ser representado por 4X2. Para
ambos os produtos a sua disponibilidade no mês nessa unidade é dum total de 720
horas.
Unidade de Montagem
e Acabamento
Para a unidade de montagem e acabamento teremos então 4X1 equivalentes a 4 horas para produto secretária e 4X2 equivalente a quatro horas para produto estantes. A disponibilidade mensal de ambos os produtos é dum total de 880 horas.
Para melhor
compreensão podemos então resumir numa tabela:
|
Secretárias |
Estantes |
CAPACITADE
DISPONÍVEL |
|
|
EU |
2
h |
4
h |
720
h |
|
UMA |
4
h |
4
h |
880
h |
2º Passo: MODELO MATEMÁTICO DE CADA UNIDADE
Da fórmula acima, podemos entender que, demora-se duas horas para o primeiro produto mais quatro horas para segundo o produto, tem que ser menor ou igual a disponibilidade Total na unidade de estampagem.
Da fórmula acima, podemos entender que, demora-se quatro horas para o primeiro produto mais quatro horas para segundo produto, o que tem de ser menor ou igual a disponibilidade Total na unidade de montagem e acabamento.
Por fim verificamos do nosso problema que a margem de lucro
da produção das secretárias e de 6kz já a produção estantes é de 3kz. A pergunta
de remate é qual é o plano de produção
mensal que maximiza a margem de lucros.
Matematicamente podemos escrever:
Que vai representar nossa Função Objetivo:
De uma forma sintética, podemos verificar que as restrições
para o nosso problema são:
q
Disponibilidade mensal na UE.
q
Disponibilidade mensal na UMA.
q
Produção mensal de secretarias.
O problema nos diz a quantidade exata de secretárias a
serem produzidas que são 160 unidades.
Concluindo, podemos escrever o nosso problema no seu modelo
matemático apoiando-se na tabela abaixo:





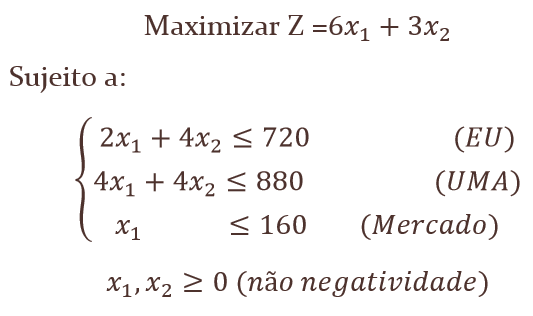
Comentários
Enviar um comentário